内挿は、既知の周囲の従属変数の値に基づいて従属変数の値を推定する数学的プロセスです。ここで、従属変数は独立変数の関数です。これは、公開されていない、または他の方法で利用可能にされていない期間の金利を決定するために使用されます。この場合、金利は従属変数であり、時間の長さは独立変数です。金利を補間するには、より短い期間とより長い期間の金利が必要になります。

ステップ1

希望の利率の期間よりも長い期間の利率から、希望の利率の期間よりも短い期間の利率を差し引く。たとえば、45日間の利率を補間していて、30日間の利率が4.2242パーセントで、60日間の利率が4.4855パーセントである場合、2つの既知の利率の差は0.2613パーセントです。

ステップ2

手順1の結果を、2つの期間の長さの差で割ります。たとえば、60日の期間と30日の期間の差は30日です。 0.2613パーセントを30日で割ると、結果は0.00871パーセントになります。

ステップ3

手順2の結果に、目的の利率の時間の長さと最短時間の利率の時間の長さの差を掛けます。たとえば、希望の利率は45日先にあり、既知の最短の利率は30日利率です。 45日と30日の違いは15日です。 15に0.00871パーセントを掛けると、0.13065パーセントになります。

ステップ4

手順3の結果を、既知の最短期間の利率に追加します。たとえば、30日間の利率は4.2242パーセントです。 4.2242パーセントと0.13065パーセントの合計は4.35485パーセントです。これは、45日間の金利の補間推定値です。

ヒント

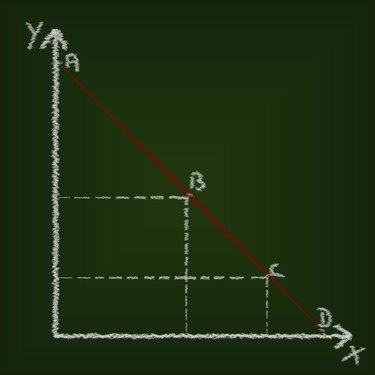
方程式に正しく従っていることを確認するために、グラフを描くことが役立つ場合があります。グラフには、一方の軸が金利を表し、もう一方の軸が時間の長さを表す必要があります。既知の金利を表す2点を通る直線を描きます。補間する金利がこの線の外にある場合は、途中でエラーが発生したことがわかります。

警告

線形補間は、特定の期間の金利の推定値であり、金利が日ごとに直線的に変化することを前提としています。実際には、金利は直線ではなく「イールドカーブ」に従う場合があります。内挿する既知の金利間の期間が短いほど、見積もりはより正確になります。

必要なもの

• 電卓

• 鉛筆

• 紙